| .. | ||
| BMP File Format.url | ||
| BMP formatas.docx | ||
| BMPImage.cs | ||
| Lab1.csproj | ||
| Program.cs | ||
| README.md | ||
| Rokas_Puzonas_IF-1-1.pdf | ||
| Test Results.xlsx | ||
| uzduotis2.png | ||
Lab1
1 užduotis
Kiekvienai rekurentinei lygčiai (gautai atlikus užduoties pasirinkimo testą):
-
Realizuoti metodą, kuris atitiktų pateiktos rekurentinės lygties sudėtingumą, t. y. programinio kodo rekursinių iškvietimų ir kiekvieno iškvietimo metu atliekamų veiksmų priklausomybę nuo duomenų. Metodas per parametrus turi priimti masyvą, kurio duomenų kiekis yra rekurentinės lygties kintamasis n (arba masyvą ir indeksų rėžius, kurie atitinkamai nurodo masyvo nagrinėjamų elementų indeksus atitinkamame iškvietime) (2 balai).
-
Kiekvienam realizuotam metodui atlikti programinio kodo analizę, parodant jog jis atitinka pateiktą rekurentinę lygtį (1 balas).
-
Išspręskite rekurentinę lygtį ir apskaičiuokite jos asimptotinį sudėtingumą (taikoma pagrindinė teorema, medžių ar kitas sprendimo metodas) (1 balas)
-
Atlikti eksperimentinį tyrimą (našumo testus: vykdymo laiką ir veiksmų skaičių) ir patikrinkite ar apskaičiuotas metodo asimptotinis sudėtingumas atitinka eksperimentinius rezultatus (1 balas).
T(n)=2 T(\frac{n}{9})+n^5T(n)=T(\frac{n}{6}) + T(\frac{n}{7}) + nT(n)=T(n-8) + T(n-6) + n
2 užduoties dalis
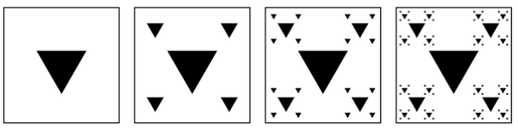
Naudojant rekursiją ir nenaudojant grafinių bibliotekų sudaryti nurodytos struktūros BMP formato ( gautą atlikus užduoties pasirinkimo testą):
-
Programos rezultatas BMP formato bylos demonstruojančios programos rekursijas. (3 balai)
-
Eksperimentiškai nustatykite darbo laiko ir veiksmų skaičiaus priklausomybę nuo generuojamo paveikslėlio dydžio (taškų skaičiaus). Gautus rezultatus atvaizduokite grafikais. Grafiką turi sudaryti nemažiau kaip 5 taškai ir paveikslėlio taškų skaičius turi didėti proporcingai (kartais). (1 balas)
-
Analitiškai įvertinkite procedūros, kuri generuoja paveikslėlį, veiksmų skaičių sudarydami rekurentinę lygtį ir ją išspręskite. Gautas rezultatas turi patvirtinti eksperimentinius rezultatus (našumo testus: vykdymo laiką ir veiksmų skaičių). (1 balas)